Midterm Exam (2)

  1. What day is the first day of a month?

    1. We have learned how to calculate the Day Number of a specific day in a month, and how to calculate what day January 1st of a specific year is.
    2. Combining the above two programs, we can easily calculate what day the first day of a month is.
    3. Suppose in a year, January 1st is on day D, and the "Day Number" of the first day of a month is N, then the first day of that month is on day (N + D - 1) % 7. (0:Sunday 6:Saturday)
      • For example, in November of 2014, D = 3 and N = 305.
    4. Write a program that accepts a date in the form "YYYY.MM" and outputs the day of the first day in that month.

    The program may run as follows:

    Input a month (YYYY.MM) -- 2014.11
The first day of 2014.11 is Saturday.

    Input a month (YYYY.MM) -- 2014.1
The first day of 2014.1 is Wednesday.

    Input a month (YYYY.MM) -- 2014.12
The first day of 2014.12 is Monday.

  2. Calendar

    1. On Unix, there is a command "cal" to print out the calendar of a specific month. For example, "cal 1 2014" prints out the calendar of January 2014. 
          January 2014
Su Mo Tu We Th Fr Sa
          1  2  3  4
 5  6  7  8  9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
    2. Develop a function cal(month_days, n) to do the following tasks:
      1. Suppose the 1st day in a month is the nth day in a week (assume Sunday is the 0th, Monday is the 1st, Wednesday is the 3rd, and so on.)
      2. Print 3*n spaces.
      3. Using a for-loop to print 1, 2, 3, ..., month_days (the possible values of month_days are 28, 29, 30, 31, depending on which month it is). If the date printed out is Saturday, output a newline (\n) character.
    3. For example, cal(31, 0) shows the following 
        1  2  3  4  5  6  7
  8  9 10 11 12 13 14
 15 16 17 18 19 20 21
 22 23 24 25 26 27 28
 29 30 31
      while cal(29, 5) shows the following: 
                       1  2
  3  4  5  6  7  8  9
 10 11 12 13 14 15 16
 17 18 19 20 21 22 23
 24 25 26 27 28 29
    4. Since we know how to calculate what day the first day in a month will be, you can directly import that function to calculate the day in a week D, then invoke the function cal(month_days, D).
    5. You may also output the name of the month, and also weekdays, to make it looks more informative. The output may look like this: 
      Input a month (YYYY.MM) -- 2014.11
November 2014
Su Mo Tu We Th Fr Sa
                   1
 2  3  4  5  6  7  8
 9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
30
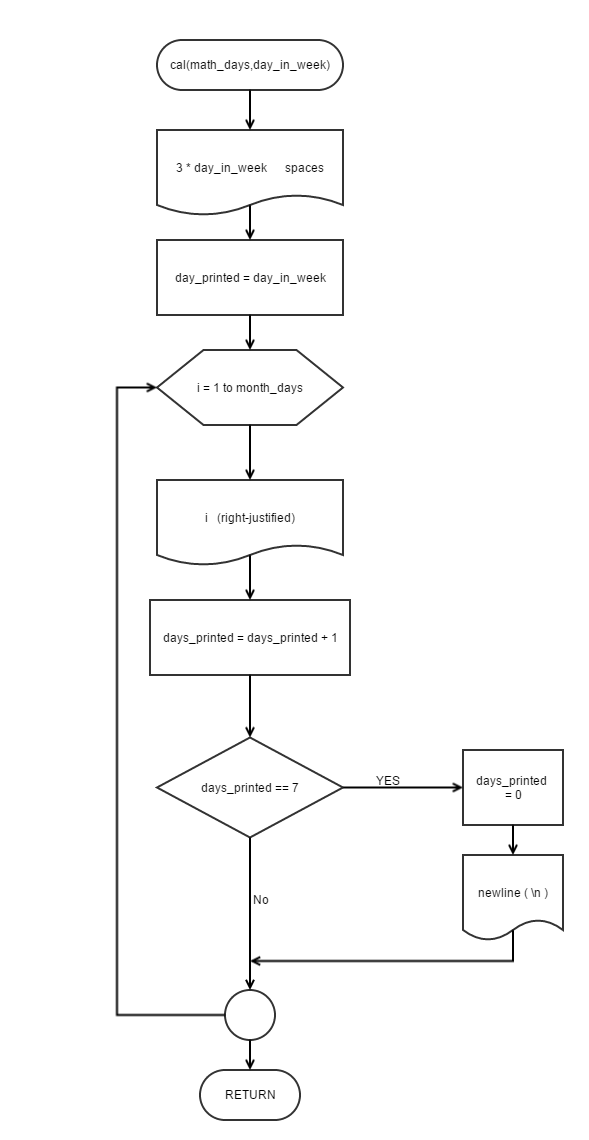    		Flowchart

  3. Prime Number

    A positive whole number n > 2 is prime if no number between 2 and sqrt(n) (inclusive) evenly divides n. Write a program that accepts a value of n as input and determines if the value is prime. If n is not prime, your program should quit as soon as it finds a value that evenly divides n.

    The program may run as follows.

    Please input a positive number -- 9
9 is not a prime number.

  4. Cycle Length of Syracuse Sequence

    1. Consider the Syracuse Sequence defined in a previous exercise.
    2. Given the input 22, the following sequence of numbers will be printed
      • 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
    3. The number of numbers printed (including the 1) is called the cycle length of a given input n.
      • For n = 22, the cycle length is 16.
    4. Design a program which requests the user to input an integer n, and then calculate the cycle length of 1, 2, 3, ..., n as follows.
    Input a number -- 22
1:1
2:2
3:8
4:3
5:6
6:9
7:17
8:4
9:20
10:7
11:15
12:10
13:10
14:18
15:18
16:5
17:13
18:21
19:21
20:8
21:8
22:16

  5. Adjusting Grades (3)

    1. Although taking the square root and multiply by 10 is a simple formula, it does not encourage students to study hard. It seems that students who have low grades benefit from this formula significantly. For example, if Alice's grade is 36, her new grade will become 60 (incremented by 24). However, if Bob's grade is 81, his new grade will become 90 (incremented by only 9).
    2. In this exercise, we shall adjust grades in a more complex way (and more realistic).
    3. Suppose the grades of students are distributed between 0 and 100 (perhaps not a normal distribution, but that does not matter). If few students get grades higher than 60, but the instructor can see that most students have studies hard, actively participated in class, and spent lots of time in writing programs, he may decide to adjust the grades so that more students can pass.
    4. The instructor will choose a threshold T (which is usually less than 60). For students whose grades are less than T, they are flunked and their grades need not be adjusted.
    5. For students whose grades are greater than or equal to T, the grade g will be adjusted by the formula: new_g = (g - T) * (UB - 75) / (max - T) + 75, where max is the maximum grade among all students, and UB is the upper-bound specified by the instructor for the adjusted grades. If the instructor decides that the highest grade in this class can be 100, he may let UB be 100. However, if the whole class does not work hard, the instructor may decide that UB can only be 89.
    6. For example, if UB = 100 and Carol's grade is equal to max, her adjusted grade will be 100. If Danny's grade is equal to T, his adjusted grade will be 75.
    7. According to this rule, it is quite possible that two students whose original grades are close, but the adjusted grades differ significant. For example, Emily's grade is 40 and Fantine's grade is 41, while T is 41. The adjusted grade of Fantine becomes 75, but Emily's grade remains unchanged. Therefore, you should see the necessity that even although you did not behave well in previous examinations, you should always try your best and work hard until the last moment. Every effort may contribute to your grade, and a little difference may help you to get passed!
    8. Modify your previous exercise about adjusting grades with this new rule. The input/output file format is the same, but the user need to supply extra parameters about T and UB at run-time. (The maximum grade can be calculated from the input file, of course.)
    9. To help the instructor to decide the value of T and UB, your program can display the maximum and average grade of the input file.

    Your program may run as follows:

    Please type the filename of student grades -- grade.txt
The maximum grade is 96
The average grade is 41.6

What would be the threshold to pass? 45
What would be the upper-bound of adjusted grades? 100
Please type a new filename to store adjusted grades -- new_grade.txt